Construction of a contour and arch with use gold
section by Dr. Vladislav Baginsky
translation by Fredrik Liden, Stockholm, Sweden
You see the basic variant of 1996 year, for outside contour.
Now I use my method for internal contour, for the models of "Stradivari"
and "Guarneri" type.
-
Decide the length of the body of the violin (Lvio = AB) = 356 mm for example.
-
Construct a rhomb with corners ADBE (the angle ADB can be chosen at will,
for example 114.592 degrees).
-
Determine the length DO = (Lvio/2)/tan(ADB/2);
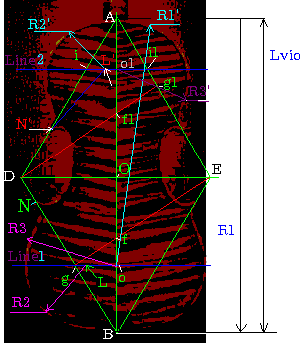 For example, if Lvio=356, DO=178/tan(57.296)=178/1.55742; DO= 114,29
For example, if Lvio=356, DO=178/tan(57.296)=178/1.55742; DO= 114,29
-
Construct the points g and g1: The lines Eg and Dg1 are drawn (perpendicular
to the lines DB and AE). Crossing these lines with a line AB defines the
points f and f1.
-
By constructing a line perpendicular to AB from the point g, we find the
point o. The line go defines the greatest width of the bottom part of the
violin (Line1).
-
Determination of the line of greatest width for the top part of the violin:
We shall consider the triangle Af1g1. The point o1 is located on the line
Af1. The position of the point o1 is defined by dividing the length of
Af1 by 1,618034 (The golden rule). This number is defined from the principle
of the golden section. If AB/BE=AE/AB,
 by substituting AB=a; BE=a/x (x is the unknown), we can write down: x=1
+ 1/x or x*x -x - 1 =0; Then x=1,6180339... In such a way we determine
a place for the point o1 and for Line2 (Ao1 = Af1 / 1.618034).
by substituting AB=a; BE=a/x (x is the unknown), we can write down: x=1
+ 1/x or x*x -x - 1 =0; Then x=1,6180339... In such a way we determine
a place for the point o1 and for Line2 (Ao1 = Af1 / 1.618034).
-
The largest width of the top of the violin is defined as io1 * 4, where
i is the point where Line2 crosses line AD.
-
The largest width of the bottom of the violin is defined as Oo * 2.
-
Constructing circles for shaping the top and bottom edges of the violin
(radii and centra for the circles are determined):
The top and bottom edges can be constructed using several circles.
For
the top part of the violin: R1'=AO (Ao - only for example!), centre
of circle at point o. R3'= io1 * 2, centre at point o1.
The circle with radius R2': We shall designate io1 * 4/1.6180339 =
Y. We should measure this distance from the edge of Line2. We shall name
one of these points L'. The second point is symmetrically placed on the
other side of AB. The point L' defines the centre of the circle with radius
R2'. The size R2'(or R2) is determined so that one gets a smooth transition
between the curves from R1'(orR1) and R3'(or R3).
For the bottom part of the violin: R1=f1 B, centre - point f1.
R3=Oo, centre at point o. R2 is constructed in the same way as R2' was
for the top part. The centre should be on Line1, and the circle segment
should describe a smooth transition from curve R1 to curve R3.
In Fig. 1 we have defined the point L' (on Line2). This point is used
to define the position of the upper corners. The length of the line L'N'
is io1 * 2 . And the point N' lies on the line DA.
Positioning the bottom corners:(see Fig. 1) The distances gN = io1
* 2. The point g is located at the crossing of Line1, the line of maximum
width of the bottom part of the violin, and the line DB. The edge between
the circle segments and the ends of the corners have to be drawn by hand.
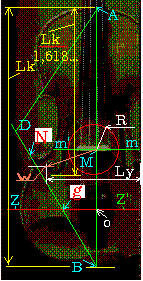 The least width
of the violin body should be on a line through the top f-hole "eye". Definition
of the distance from the top edge of the violin down to the location of
the bridge (also known as the mensur). We call this distance AM. AM/Af1
= Lvio/AM; AM = (Lvio * Af1) **(1/2), [i.e. the square root of (Lvio *
Af1)]. The point M is the centre of the circle with radius R. For a violin
we can choose the radius R = 36 mm. The centre of the top f-hole "eyes"
lies on the circle R. The innermost edges of the f-holes touch the circle
R at the point where the line m'm intersects the circle R. This is where
the inner notches in the f-holes are placed. The bridge is located on the
line m'm.
The least width
of the violin body should be on a line through the top f-hole "eye". Definition
of the distance from the top edge of the violin down to the location of
the bridge (also known as the mensur). We call this distance AM. AM/Af1
= Lvio/AM; AM = (Lvio * Af1) **(1/2), [i.e. the square root of (Lvio *
Af1)]. The point M is the centre of the circle with radius R. For a violin
we can choose the radius R = 36 mm. The centre of the top f-hole "eyes"
lies on the circle R. The innermost edges of the f-holes touch the circle
R at the point where the line m'm intersects the circle R. This is where
the inner notches in the f-holes are placed. The bridge is located on the
line m'm.
Additional information: In many cases the distance Lk/1,6180339 is equal
to the distance from the top edge of the violin to the bottom edge of the
lower f-hole "eyes"
The point i on the line AD can be determined as: AD/1,6180339. The
distance Ly can vary slightly; Ly=130 +/-1mm; MW = 2R
The above described way of constructing a violin has been tried by several
violin makers, and has been found to be quite successful. It is also possible
to apply this method when constructing violas. The author welcomes comments
regarding this method of construction.
Method for constructing an arched
violin top plate.
by Vladislav Baginsky, Odessa.
(translation by Fredrik Liden, Stockholm, Sweden)
The construction of the arch is based on the assumption that the shape
of the central surface of the violin front plate can be approximated by
a cylindrical surface. The following table refers to a violin front plate
of 356 mm total length, and 17.5 mm highest arch:
| Distance from top of front plate |
Arch height |
Cylinder radius |
Width |
Comments |
| 69.5 mm |
13.8 mm |
356 mm |
169 mm |
Widest part of top |
| 118 mm |
16.3 mm |
160 mm |
154 mm |
- |
| 157 mm |
17.5 mm |
124 mm |
110 mm |
Narrowest part of plate |
| 224 mm |
16.5 mm |
157 mm |
179 mm |
- |
| 286 mm |
13.2 mm |
466 mm |
211 mm |
Widest part of bottom |
If the above measurements 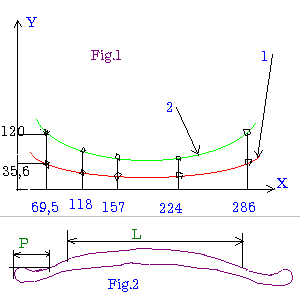 are plotted in a x-y diagram with distance on the x-axis and cylinder radius
on the y-axis one can fit a smooth curve which will describe the desired
surface of the violin. Line 1 describes the outside surface of the violin
front plate, and line 2 describes the shape of the inside surface.
are plotted in a x-y diagram with distance on the x-axis and cylinder radius
on the y-axis one can fit a smooth curve which will describe the desired
surface of the violin. Line 1 describes the outside surface of the violin
front plate, and line 2 describes the shape of the inside surface.
The edge thickness of the plate should be 4.2 mm, except at the middle
bouts where it should be 4.5 mm all the way from the top to the bottom
corner block positions.
The area close to the edges where the channel is situated can not be
described with the cylindrical surface model.
The width of the violin front plate where the cylindrical model can
be applied is described in the table below:
| Distance from top of front plate |
Width (L) |
Cylinder radius |
Distance from edge (P) |
Comments |
| 69.5 mm |
123 mm |
356 mm |
10 mm |
Widest part of top |
| 118 mm |
63 mm |
160 mm |
14 mm |
- |
| 157 mm |
53 mm |
124 mm |
6.5 mm |
Narrowest part of plate |
| 224 mm |
80 mm |
157 mm |
15 mm |
- |
| 286 mm |
147 mm |
466 mm |
10 mm |
Widest part of bottom |
Note that the characteristic sizes of the contour of the violin plate differs
from the values obtained when using the "golden rule".
This method should not be used in publications without the consent
of the author.
Look also: Robert Zuger-
"The original design of the violin"
Look also other books:
Geometric Model Of The Violin by C. Kjellgren This book details and
illuminates the geometry of violins.
Geometric Model Of The Violin by C. Kjellgren
This book details and illuminates the geometry of violins.
Heron-Allen, Edward. VIOLIN-MAKING: AS IT WAS AND IS; Being a Historical,
Theoretical, and Practical Treatise on the Science and Art of Violin-Making,
for the Use of Violin Makers and Players, Amateur and Professional. London,
1991.
xix, 366 pp., frontispiece, 5 illustrations, 196 wood-cuts, 3 fold-out
diagrams. (facsimile reprint) $65.00
Heron-Allen, Edward. DE FIDICULIS BIBLIOGRAPHIA: Being the Basis of
a Bibliography of the Violin and All Other Instruments Played with a Bow
in Ancient and Modern Times. London: Griffith, Farran, Okeden & Welsh,
1890-1894.
x, 416 pp., lxxviii, (one side only) with a total of 1236 entries,
plus 241 entries in the suplements, and an index by author and subject,
plus an appendix and list of errata. Six parts and 4 supplements, originally
published in 12 separate pamphlets over a period of 4 years. Part I, Section
I: The Construction of the Violin. Part I, Section II: Biographical Works,
and III: Works on Varnish. Part I, Section IV: The History of the Violin.
Part I, Section V: Theoretical Works, with Supplement. Part II: Book Sections
and Extracts. Part II: Book Sections and Extracts (continued) and Second
Supplement. Part III: Periodical Publications. Part IV: Belles Lettres.
Part V: Methodes and Instruction. Part VI: Miscellanea. Third Supplement.
Fourth Supplement. The first two parts are in the original separate parts.
The remaining parts, III-VI, plus the supplements are included in the 2nd
volume of the deluxe two volume edition. (This 2nd volume is unopened,
with the spine and the edges of the covers a bit frayed) This is one of
the rarest of all books on the the violin family, and a very valuable reference
book. (It has now been updated by Roberto Regazzi in his book, The Complete
Luthier's Library, but is remarkably complete for 1894!) Extremely scarce.
$750.00
Henley, William and Woodcock, Cyril. ANTONIO STRADIVARI. Master Luthier.
Cremona, Italy, 1644-1737. His Life and Instruments. London: Amati Publishing
Ltd., 1961.
97 pp., 95 plates of instruments. (covers sprung, d.j. worn, signed
by Woodcock) Lists all known Strads and various owners, giving details
of varnish, tone, model, measurements and in many cases, prices paid in
the past and present. $50.00
The Acoustical Systems Of Violins & Stradivarius & Other Cremona
Violin Makers by Isaak Vigdorchik Aculmination of over 30 years of work
as a performer and maker. It presents a rational and convincing explanation
of the way in which the Cremona Masters tuned their plates, the most important
of the variables that contribute to the acoustical phenomenon that is the
violin.
Sacconi, Simone F. THE SECRETS OF STRADIVARI. Cremona, 2000.
xviii, 265 pp., 3 color plates, 182 figures, portrait. In English.
(fine condition) New printing. $150.00
The Secrets of Stradivari by Simone F. Sacconi This attractively hard
bound edition has not been available since 1996. An improvement on the
original translation from Italian to English by Andrew Dipper, this reprint
deals with violin and varnish and its application with designs of various
instruments. Many illustrations of instrument patterns, also models and
tools used by Stradivari.
Davidson, Peter. THE VIOLIN: Its Construction Theoretically and Practically
Treated; Including an Epitome of the Lives of the Most Eminent Artists,
a Dictionary of Violin Makers and Lists of Violin Sales. London: F. Pitman,
1881. New edition, revised and considerably enlarged.
viii, 268 pp., 31 illustrations, fold-out. (4 1/2 x 6 3/4 inches, covers
sl. sprung, covers a bit worn and spotted, a few pages partially loose)
An interesting little book which includes a few varnish recipes. Scarce!
Foucher, G. TREATISE ON THE HISTORY & CONSTRUCTION OF THE VIOLIN.
With a Short Account of the Lives of its Greatest Players and Makers. London,
1894. First edition. (viii) 82 pp. (4 1/4 x 6 1/4 inches, sl. wear, sl.
sprung)
Giltay, J. W. BOW INSTRUMENTS. Their Form and Construction. Practical
and Detailed Investigations and Experiments Regarding Vibration, Sound
Results & construction. London, n.d. x, 129 pp., 57 figures. (8vo,
cloth, covers sl. stained)
Gosling, Henry F. THE VIOLINIST'S MANUAL. A Treatise on the Construction,
Choice, Care, Adjustment, Study and Technique of the Violin. London: William
Reeves, n.d.
xv, 270 pp., frontis. (fold-out), 40 plates, musical examples. (some
wear) Includes information on the origin, construction and adjustment of
the violin and bow, study and care of the violin, and the techniques of
performance.
'F' Hole Models by
Hans Elder This hard bound book has 71 pages of 124 illustrated sound holes
from the most famous makers; from Amati to Zanoli. An ideal reference book
for those interested in identifying makers through this medium.
A Luthier's Scrapbook by H. S. Wake
A 112 page soft bound collection of short "how to do it" articles and
bits of information pertaining to the making and restoration of instruments
of the violin family. Second edition with drawings by the author.
The Technique Of Violin Making by H. S. Wake
Over one hundred 8" X 11" profusely illustrated pages, plus six pages
10" X 16" full scale working drawings describing the making of a violin
from start to finish.
Practical Violin Making by E. Frazer
This booklet contains 23 pages with dozens of drawings of violin parts,
tools, etc... Included are two sheets of full sized templates of the 1920
Strad model. Ideal for the beginner.
Useful Measurements For Violins Makers by Henry A Strobel
Revised second edition. A standard reference that is unique and comprehensive.
Size and adjustment information for full sized and fractional sized instruments;
violins, viola, cello and bass. Includes bridge templates with concise
explanations of key points of interest and use to anyone who makes and
repairs violins or is otherwise professionally involved with bowed instruments.
Cross reference of 200 violin terms in four languages.
The International School Of Cremona Two Score Years Of Violin
Making by Gualtiero Nicolini
This beautifully bound publication traces the history of this prestigious
institution from its inception to the present day. It is fully illustrated,
including instruments of the Cremona Museum and those of its celebrated
faculty, graduates and students. English text.
An A To Z Of Instrument Care For Players Of The Violin Family
by Jane Dorner
This pocket sized 48 page soft cover combines a first aid manual and
good health for every string player's most precious possession. Defines
the limits of self-help and when to seek professional advice.
Bonetti, Carlo, Cavalcabo, Agostino, and Gualazzini, Ugo. ANTONIO STRADIVARI.
Reports and Documents. 1937. Cremona: Cremonabooks, 1999.
xiv, 104 pp., illustration. (8vo, stiff paper covers) The new translation
of this important book. $35.00
Fetis, F. J. NOTICE OF ANTHONY STRADIVARI. The Celebrated Violin-Maker,
Known by the Name of Stradivarius. London: Robert Cocks and Co., 1864.
First English edition.
xiv, 132 pp., numerous illustrations. (5 3/4 x 8 7/8 inches, covers
sl. worn, spine sl. frayed) This edition scarce. $150.00
ALL RIGHTS PROTECTED Vladislav Baginsky,
Ukraine, Odessa.
Русская версия текста
(Mehtod on Russian, (use koi8-R code)
Метод построения контура и свода скрипки
с использованием золотого сечения. Использование
в открытой печати недопустимо без согласия автора.
Этот способ разработан мной в1995 году. В настоящее время я применяю
свой метод для внутреннего контура, для модели "Страдивари " и " Гварнери".
Некоторые дальнейшие изменения отмечены наклонным шрифтом.
-
Выбор длины корпуса скрипки Lvio =AB(по решению мастера), 356 мм для примера.
-
Построение ромба с углом ADB =57,296*2=114,592 или другим, выбираемым по
желанию.

-
Определение длины DO= Lvio/2tg 57,296; Например, если Lvio=356 , то DO=356/2*1,55742;
DO=114,29
-
Построение точки g и точки g1: Рисуются линии Eg иDg1, перпендикулярно
к сторонам DB и AE. Пересечение этих линий с линией AB определяет точки
f и f1.
-
Построив перпендикуляр к линии AB из точки g , мы получим точку о. Линия
go определяет место самой большой ширины нижней окружности скрипки .
-
Определение линии максимальной ширины верхнего « овала» скрипки: Рассмотрим
прямоугольный треугольник Af1g1. Точка o1 расположена на стороне Af1. Положение
точки o1 определяется в результате деления длины отрезка Af1 на число 1,618034.
(точные размеры можно определить из тригонометрических соотношений). Что
это за число: 1, 618034? Это число можно определить из принципа золотого
сечения. Если AB/BE=AE/AB , то написав , что AB=a; BE=a/x (x-неизвестная),
мы можем записать: x=1+1/x или x*x -x - 1 =0 ; Тогда x=1,6180339...
-
Линия определяющая самую большую ширину верхнего овала скрипки может быть
определена из рассмотрения треугольника Af1g1. Длину Af1/1,6180339 необходимо
отмерить от места, где находится точка A . В результате этого мы определим
место расположения точки o1 и линии № 2.
-
Самая большая ширина верхней окружности скрипки (верхнего овала) равна
io1*4.
-
Самая большая ширина нижней окружности равна Oo*2 .
-
Определение расстояния от верхнего края скрипки до места расположения подставки.
Обозначим это расстояние как AM. AM/Af1=Lvio/AM; AM=(Lvio*Af1)**(1/2) .
-
Нахождение радиусов для верхней и нижней окружностей и мест расположения
осей вращения этих радиусов. Верхний и нижний « овал» скрипки может быть
построен из нескольких радиусных кривых. Для верхней части скрипки:
R1'=AO, (на рис.1 - Ao, только для примера) ось вращения в точке O
. Протяженность радиусной кривой примерно равна длине верхнего клотца.
-
R3'= io1*2 ,ось вращения - точка o1 . (Для множества случаев, для
скрипки R3'=fo1*2 ). Ось вращения для R2' : Обозначим io1*4/1,6180339=Y.
Мы должны отмерить это расстояние от точек определяющих самый большой размер
(максимальную ширину) верхнего овала скрипки. Мы обозначим одну из этих
точек L'. Вторую точку можно не рассматривать , она симметрична. Точка
L' определяет ось вращения R2'. Величина R2' определяется экспериментально,
из условия плавного перехода, (сопряжения) между кривыми R1' и R3'. Для
нижней части скрипки: R1 = f1 B , ось вращения - точка f1. R3=Оo, ось
вращения -точка O. R2 определяется по аналогии , ось вращения определяется
методом проб. Определение границы верхних углов: Для Fig2 , мы нашли расположение
точки L' (на линии ii'). Отрезок L'N'= io1*2 .Точка N' должна находится
на линии DA . Определение места расположения нижнего угла : Расстояние
gN= io1*2 . Точка g расположена на пересечении линий максимальной ширины
нижнего овала (ZZ') и линии DB . Сопряжения между радиусными кривыми и
окончаниями углов необходимо вычерчивать карандашом.
ОПРЕДЕЛЕНИЕ МЕСТА РАСПОЛОЖЕНИЯ ЭФОВ
Построение эфов производится вручную, выбрав предварительно размер
талии. Наименьшая ширина талии должна находиться на линии самых верхних
точек эфов. Точка M является осью для вычерчивания круга. Для скрипки мы
можем выбрать радиус круга R=36 mm. На линии круга находится середина верхнего
глазка эфа. С этой линией соприкасается одна из линий эфов, на которой
расположена зарубка. Середина внутренних зарубок эфов пересекают линию
mm', точка M расположена в центре круга . Дополнительная информация:
(Во многих случаях для скрипки Lk/1,6180339 равно расстоянию от верхнего
края деки до нижней части нижнего глазка эфа. (Это расстояние измеряетcя
по линии вертикальной оси скрипки.) Расстояние МW = 2R
 Точка i на линии
DA может быть определена как:
Точка i на линии
DA может быть определена как:
DA/1,6180339; Расстояние Ly меняться может очень незначительно.
Ly=130+-1mm
Вы можете прислать мне ваши впечатления о моем методе. Возможно вы
увидите пути усовершенствования, не стесняйтесь написать также.
Этот метод можно использовать и для построения контура альта также.
ПОСТРОЕНИЕ СВОДА
Построение свода основывается на предположении , что средняя часть
поверхности свода скрипки,(между эфами) на некоторой ее протяженности,
очень близка к цилиндрической поверхности. Тогда можно предположить, что
области верхнего и нижнего овалов скрипки имеют также некоторые площади
поверхности приближающиеся к цилиндрическим . Далее Вы прочтете описание
построения такого свода, для модели скрипки с следующими характерными размерами:
Длина верхней деки - 356 мм, свод с высотой 17,5 мм ; Наибольшая ширина
верхнего «овала» - 169 мм, на расстоянии 69-70 мм от верхнего края деки,
высота свода - 13,8 мм , толщина края = 4,2мм ; Наибольшая ширина нижнего
овала - 211 мм, на расстоянии 286 мм от верхнего края деки , высота свода
= 13,2мм , толщина края = ,2мм; Наименьшая ширина верхней деки - 110 мм,
над верхними глазками эфов, на расстоянии 157 мм от верхнего края деки,
высота свода = 17,5 мм, толщина края=4,5 мм ; Наибольшая ширина верхней
деки на расстоянии 118 мм от верхнего края деки = 169 мм , высота свода
= 16,3 мм , толщина края = 4,2 мм) ; Наибольшая ширина верхней деки на
расстоянии 223-224мм от верхнего края деки =13,2мм высота свода 16, 5-16,6
мм ,толщина края = 4,2мм ; Толщина краев деки на всей протяженности от
верхних до нижних углов = 4,5 мм. Все размеры высот свода для квинт кривизны
хорошо согласуются между собой, что видно из графика, где по оси Y мы можем
отмерить значения радиусов кривизны поверхности , уменьшенных в десять
раз (в миллиметрах), а по оси X - значения расстояний от верхнего края
деки, для соответствующих квинт кривизны. (Рис.1 )
| Расстояние от верхнего края деки |
Высота свода |
Радиус кривизны |
Высота |
Примечание |
| 69.5 mm |
13.8 mm |
356 mm |
169 mm |
Широкая часть верхнего овала |
| 118 mm |
16.3 mm |
160 mm |
154 mm |
- |
| 157 mm |
17.5 |
124 mm |
110 mm |
В самой узкой части |
| 224 mm |
16.5 mm |
157 mm |
179 mm |
- |
| 286 mm |
13.2 mm |
466 mm |
211 mm |
Широкая часть нижнего овала |

Большое значение для акустики скрипки имеет место перехода выпуклости
в вогнутость в квинте кривизны.
Используя число 1,6180339 (часто употребляемое число при построениях,
с использованием принципа золотого сечения) и комбинации разностей между
длиной деки и расстоянием от верхнего края до квинт кривизны , можно получить
множество значений длин и использовать их при построениях.
Некоторые из этих значений вполне подходят для нашей задачи определения
величины L. (Рис.2)
Я предлагаю следующие значения величины L:
| Расстояние от верхнего края деки |
Высота (L) |
Радиус кривизны |
Расстояние от края (P) |
Примечание |
| 69.5 mm |
123 mm |
356 mm |
10 mm |
Широкая часть верхнего овала |
| 118 mm |
63 mm |
160 mm |
14 mm |
- |
| 157 mm |
53 mm |
124 mm |
6.5 mm |
Самая узкая часть |
| 224 mm |
80 mm |
157 mm |
15 mm |
- |
| 286 mm |
147 mm |
466 mm |
10 mm |
Широкая часть нижнего овала |
Эти значения мы можем использовать для построения кривой № 2
на рис.1. В данном случае на оси Y необходимо отложить предложенные значения
L , в мм. Координаты точек на оси X прежние. Важное значение имеет предварительный
выбор длины плоского участка деки, у края деки. Многие мастера вырабатывают
необходимую толщину краев и расстояние ( « P « ), при помощи вращающейся
дисковой фрезы расположенной над плоским столом , на фиксированном расстоянии
от него (например 4,2мм). Длина "P" устанавливается при помощи дополнительных
насадок различного размера. Я предлагаю следующие размеры длины "Р" верхней
деки: Для верхнего и нижнего края Р=10 мм. См. также Robert
Zuger- "The original design of the violin"
Сайт управляется системой
uCoz For example, if Lvio=356, DO=178/tan(57.296)=178/1.55742; DO= 114,29
For example, if Lvio=356, DO=178/tan(57.296)=178/1.55742; DO= 114,29 The least width
of the violin body should be on a line through the top f-hole "eye". Definition
of the distance from the top edge of the violin down to the location of
the bridge (also known as the mensur). We call this distance AM. AM/Af1
= Lvio/AM; AM = (Lvio * Af1) **(1/2), [i.e. the square root of (Lvio *
Af1)]. The point M is the centre of the circle with radius R. For a violin
we can choose the radius R = 36 mm. The centre of the top f-hole "eyes"
lies on the circle R. The innermost edges of the f-holes touch the circle
R at the point where the line m'm intersects the circle R. This is where
the inner notches in the f-holes are placed. The bridge is located on the
line m'm.
The least width
of the violin body should be on a line through the top f-hole "eye". Definition
of the distance from the top edge of the violin down to the location of
the bridge (also known as the mensur). We call this distance AM. AM/Af1
= Lvio/AM; AM = (Lvio * Af1) **(1/2), [i.e. the square root of (Lvio *
Af1)]. The point M is the centre of the circle with radius R. For a violin
we can choose the radius R = 36 mm. The centre of the top f-hole "eyes"
lies on the circle R. The innermost edges of the f-holes touch the circle
R at the point where the line m'm intersects the circle R. This is where
the inner notches in the f-holes are placed. The bridge is located on the
line m'm.
 are plotted in a x-y diagram with distance on the x-axis and cylinder radius
on the y-axis one can fit a smooth curve which will describe the desired
surface of the violin. Line 1 describes the outside surface of the violin
front plate, and line 2 describes the shape of the inside surface.
are plotted in a x-y diagram with distance on the x-axis and cylinder radius
on the y-axis one can fit a smooth curve which will describe the desired
surface of the violin. Line 1 describes the outside surface of the violin
front plate, and line 2 describes the shape of the inside surface.